The main aim of this paper is to investigate how the production-rule-based computational paradigm can be implemented through visual data-flow techniques. Since building production rules solving a problem may be a difficult task for an unskilled beginner programmer and a textual-only rule representation may not turn out to be very intuitive, we propose a simple yet effective system for visually composing rule preconditions and actions, through a general purpose data-flow visual language. This system, which is primarily intended as a learning tool, can greatly simplify the programmer's task and speed up the implied reasoning process. Moreover, it allows production-rule-based programs to be easily integrated within more general applications.
Although the debate about the usefulness of visual programming languages compared with textual ones is quite far from being over, it is indisputable that, at least for certain applications, interacting with objects placed in a two-dimensional space may be extremely worthwhile [1]. In fact, graphic elements have the advantage of being characterized by shape, dimension, position and possibly color, all attributes which may help better understand the meaning of what is displayed on the screen. Thus, for example, in [2] it is claimed that pictures are superior to text, since they are abstract, instantly comprehensible and universal and in [3] it is argued that diagrams can support and optimize reasoning thanks to their ability to model whole-part relations.
As far as we are concerned, we think that visual programming (VP), if properly exploited, holds very great potential and can speed up reasoning processes. By VP system we mean one which satisfies the two following criteria [4]: 1) it executes, and 2) it allows specification of programs to be modified within the visual environment. Functional and logic programming has also taken advantage of the visual approach: for example, GARDEN [5] is a visual system based on Lisp, while VLP [6] and VPP [7] are visual implementations of Prolog-like reasoning.
Among general purpose VP systems, data-flow ones (such as LabView [8]) are very widespread, certainly also thanks to their simple and intuitive functioning mechanism. Essentially, a data-flow visual program is a graph in which the data tokens travel along arcs between nodes (graphic elements representing functions) which in turn transform the data tokens themselves.
It is very interesting to note that the data-flow model may be viewed as a generalization of the event-driven programming model [4]: each node waits for data (events) to arrive and then fires. Hence, production-rule systems can also be viewed as data-flow systems, in which rule conditions act as demons awaiting the arrival of certain data elements before executing their conclusion.
Production systems are the basis for many expert systems. However, their functioning mechanism may be especially difficult to understand for those who are used to programming according to the control-flow (imperative) paradigm. Building correct productions to solve a particular problem is a task which may require many attempts by an unskilled programmer (addition and elimination of conditions and/or actions). Very often, different rules hold the same preconditions, and comprehension of the way they affect the global system may depend on just such a sharing.
A textual-only rule representation may turn out to be very unintuitive. For example, confirming the importance of a bidimensional transposition of rules for their easy understanding, Gaines and others tackle the problem of transforming the knowledge base of rule-based expert systems into comprehensible knowledge structures, through graphic representations [9]. We may also quote, among other works, Cartoonist [10], a rule-based visual programming environment used to build simulations, which are described in terms of combinations of simple behavioral patterns of the objects in the simulations themselves.
This paper will show how it is possible to easily implement the production-rule-based computational paradigm by using visual data-flow techniques. The simple but effective system we will describe, which is based on VIPERS [11], a general-purpose data-flow visual language, is primarily intended as a learning tool and can greatly simplify the task of the novice production-rule programmer. In fact, visual combination of preconditions and actions, by allowing productions to be graphically assembled, ensures greater intuitiveness and simplicity during the phases of creating rules and testing their influence on the whole program. Even though we are aware that the visual system we are proposing becomes difficult to use when more than five or six productions are involved, because of the several links necessary to connect VIPERS components, we think it can anyway be very useful at the very beginning of the learning stage. Moreover, we believe that our approach is particularly interesting from a theoretical point of view.
The article is structured as follows: Section 2 presents a brief overview of the VIPERS environment. Section 3 explains the basic assumptions on which our system is based. Section 4 describes the proposed visual approach and its main characteristics. Section 5 discusses how conditions and actions can be implemented through VIPERS blocks. Section 6 presents some comments about the proposed approach. Section 7 formalizes block functionalities. Section 8 shows a simple practical example of rule visually assembling. Section 9, at last, concludes the paper with final considerations.
The system we use for building production-rule-based applications is VIPERS [11], a general-purpose visual programming environment based on an augmented data-flow model and developed at the University of Pavia.
VIPERS uses a single interpretive language (Tcl [12]) to define the elementary functional blocks (the nodes of the data-flow graph). Each block corresponds to a Tcl command (or procedure).
VIPERS elementary modules have a square shape and present connection points, or ports, on their lateral sides; programs are assembled in a direct manipulation fashion, by positioning and properly connecting the available modules. Entire programs may therefore be built without typing any line of code: after having found in a certain window the needed functions (the nodes of the graph), which are represented by special icons, the programmer simply drags and drops them into the main workspace: a couple of simple mouse-clicks are then sufficient to create an arc between two nodes. The particular box-line representation allows proper viewing monitors to be easily inserted at various points of the program to show partial results to the user.
The system we are describing also uses some textual information, which has to be written: indeed, it is reasonable to combine visual and textual languages to exploit the best from each [13]. In the remainder of this section, the basic data representation assumptions on which the system is based will be discussed.
An associative system for symbolic computing is basically composed of a working
memory, a production memory and an interpreter. Briefly,
we may consider working memory (WM) as an ordered collection of pairs:
tag : symbolic structure, where tag is an integer
number defining order and symbolic structure is any constant
symbolic list (such as, for instance: "goal a 4" or "position
{b1 b2}"). For our system, we denote WM's elements by means of Tcl lists
of the kind: { tag { symbolic structure } }.
Production memory (PM) is a non-ordered collection of computational structures of the type:
preconditions
=>
actions
Preconditions, which are logically ANDed, are expressed by symbolic list
patterns, possibly containing variables. To denote variables we choose, for
example, to place a question mark before them, like in ?x. We
identify preconditions by means of lists of the kind: { symbolic
structure } or { ?t { symbolic structure } }, where
?t is a generic variable designating the tag of that WM's element
which matches symbolic structure (this variable is necessary when it is
important to distinguish between different elements satisfying the same
condition). Moreover, we admit test expressions, that is ordinary Tcl logical
expressions (possibly containing variables and Tcl commands, like for action
ADD, which will be discussed later) placed in list structures of the
form: { test { test expression } }. Actions can be:
| ADD symbolic structure : | adds symbolic structure to WM; |
| DEL symbolic structure : | deletes symbolic structure from WM; |
| DEL n : | deletes from WM that element matched by the n-th condition of the activated production; |
| ACTION : | executes an action which is independent of WM; |
where symbolic structure may contain variables, in whose place the
respective values are substituted, according to the bond environment created
during precondition analysis. In the case of the ADD, moreover, symbolic
structure may contain Tcl commands as well, enclosed in braces. In order to
distinguish lists representing Tcl commands, we choose to place the character
# before them, like, for example, in:
cur_state #{list #{expr ?x+?y*2} 1}.
We indicate an exemplar of a production P with the list {P
tag1 ... tagn}, where tag1 ... tagn are
those WM elements' tags matching conditions 1 ... n of the production.
Conflict set (CS) is the set of all those production exemplars which, at a certain time, can be activated.
The interpreter (inferential engine) determines system evolution. During every computational cycle it constructs CS, chooses a production exemplar according to a particular selection strategy and executes those actions concerning the selected production. Computation ends when CS is empty.
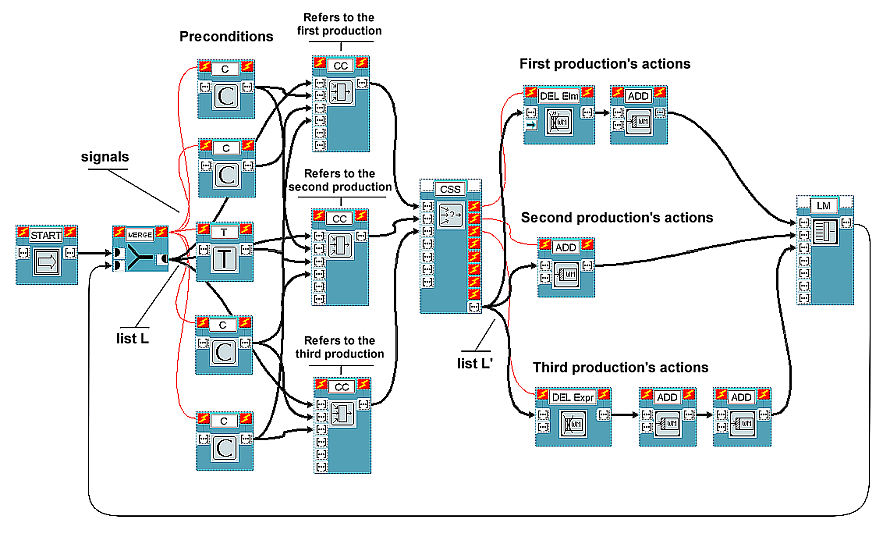
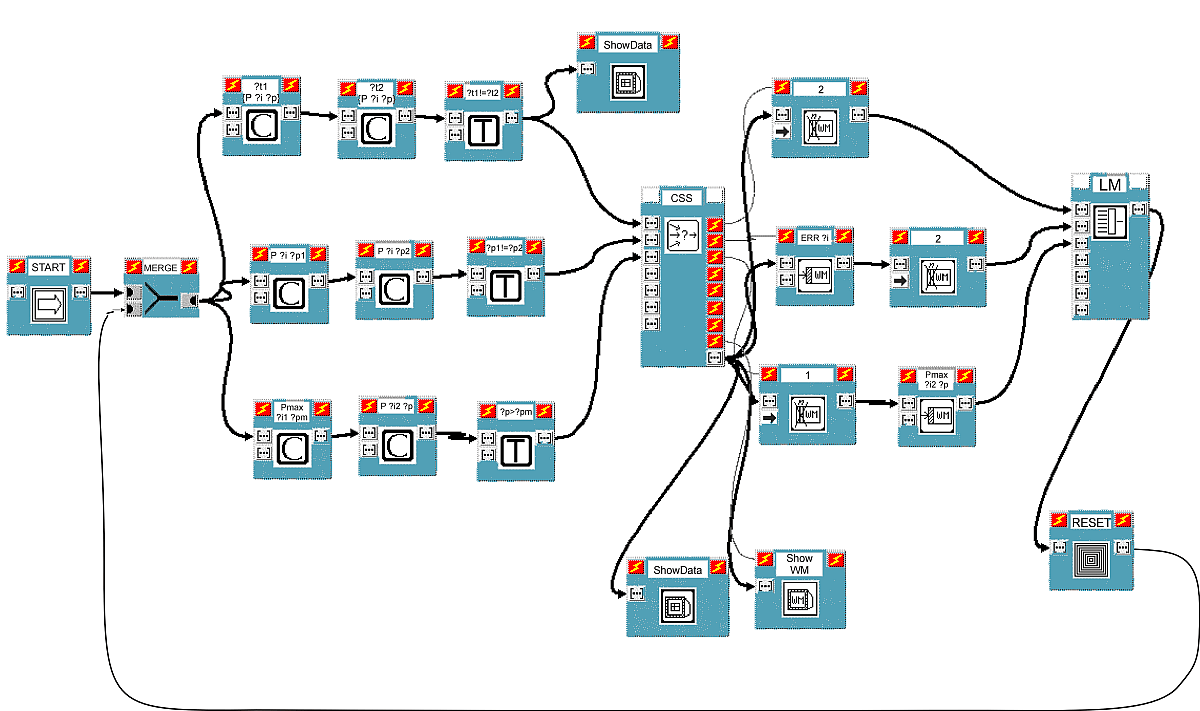
We propose two substantially equivalent ways to visually build productions. The former is shown in Figure 1 and better highlights distribution of conditions being shared by different rules. The latter, which will be shown afterwards, gives up this opportunity but is probably more readable.

As can be seen from Figure 1, each input/output port in VIPERS is
characterized by a special icon indicating the corresponding data type. Icons
for data types used in our system are [...] (which represents a
list, that is any sequence of characters) and -> (which
represents an integer value).
The MERGE block fires when either of its two input ports receives a new data item, which is then emitted as an output. Block START gives out initial data.
To achieve correct synchronization, VIPERS exploits control signals (thin arcs without arrows) connecting blocks control ports (those with the lightning symbol). If a signal exists between an output control port (on the right) of block A and the input control port (on the left) of block B, then block B cannot be executed before the execution of block A. For example, with reference to Figure 1, blocks C and T are activated by execution of block MERGE. All block functionalities are implemented in Tcl.
Figure 1 shows an example scheme composed of three productions. Condition blocks C and Test blocks T represent rule preconditions and, when activated, limit themselves to giving out symbolic lists that denote them. The way conditions, tests and actions can be specified will be described in Section 5.
There is a Condition Collector block CC for every rule. CC blocks analyze the respective input conditions to determine whether the rule is applicable or not (that is, whether at least one production exemplar exists relative to the rule). Every CC block has another list as input, which we will call L. It is the data structure which is propagated to CC blocks outputs, after being "filled" with information deriving from precondition analysis. During the next computational cycles, it will return to the same blocks, with some changes (unless the program is finished). The structure of list L is:
L = {ok WM ENVs TAGs ActExs n_cond n_test max_t}
where the various elements have the following meanings:
ok: |
is a flag indicating whether list data is to be considered valid or not; |
WM: |
is a list of the type {wm_el1
... wm_eln}, where
wm_eli represents the
i-th working memory's element (we remind that wm_eli
= {tagi {symbolic
structure}} );
|
ENVs: |
is a list of the kind {{e1}
...{em}}, where
ei
is the bond environment relative to the i-th exemplar which can be built
with the specific production (several matching possibilities may exist
between a production's preconditions and working memory elements).
ei is simply a sequence
var1i
val1i ... varsi
valsi, var being the variable's name
and val its value;
|
TAGs: |
is the list of all those production exemplars which have been already
activated in previous computational cycles and serves to allow block CSS
to exclude them from the conflict set, when the lex selection strategy
is chosen, as will be discussed later. The structure of this list is of
the type {{pn t1 ... t
pn_cn}1
... {pn t1...
tpn_cn}q},
where pn is an integer number identifying the
production and t1 ... tpn_cn
the sequence of the exemplar's tags (which are the same number as the
number pn_cn of production pn's conditions);
|
ActExs: |
is the list of all those production exemplars which have been already
activated in previous computational cycles and serves to allow block
CSS to exclude them from the conflict set, when the lex selection
strategy is chosen, as will be discussed later. The structure of this
list is of the type {{pn t1
... tpn_cn}1 ...
{pn t1 ...
tpn_cn}q},
where pn is an integer number identifying the production
and t1 ... tpn_cn
the sequence of the exemplar's tags (which are the same number as the
number pn_cn of production pn |
n_cond: |
indicates the number of the specific production's conditions; |
n_test: |
indicates the number of the specific production's test conditions; |
max_t: |
ndicates the maximum tag value present in working memory. |
Elements WM, ActExs and max_t are not
modified by CC blocks, while the others reflect the analysis carried out for
the specific production.
The choice of placing data represented by the just described elements into a single list is particularly advantageous for the programmer, who, during visual program construction, can restrict him/herself to connecting only a few outputs with few inputs.
The task of block CSS (Conflict Set Solver) is to choose which production exemplar, among the possible ones, is to be activated, according to a certain selection strategy. Several CSS blocks will be put at the programmer's disposal, so that he/she can easily select the desired strategy. Among feasible ones, we remind the following:
Block CSS receives the various L lists emitted by CC blocks as inputs.
According to the value of flag ok which is present in such lists,
it realizes whether the corresponding productions have created exemplars,
that is whether lists' data are to be considered or not. On the basis of data
contained in valid lists, CSS applies the selection strategy it represents
and activates only that output signal relative to the chosen production
action sequence or, in case of null conflict set, the last one, which powers
up one or more end blocks (in Figure 1, block ShowWM, showing the
WM's contents). Moreover, CSS gives a list L' out with the same structure as
L, except for the fact that elements ENVs and TAGs
have been substituted with that environment and that tag sequence referring
only to the sole selected exemplar, which has been added to ActExs.
List L' provides actions with the data to act on.
The programmer can use three different kinds of standard action blocks (one
for ADD and two for DEL), plus an arbitrary number of blocks relative to
actions not modifying working memory and definable according to the
particular sort of application. Every action block receives L' as input list
and, at most modifying elements WM and/or max_t,
then gives it out. The output of the last action block executed enters block
LM (Lists Merge), comes out of it without any change, goes
into the initial block MERGE and, at last, submits itself to the CC blocks
again. CC blocks and block CSS can be built with as many input ports as one
likes so that there is no fixed limit to the number of preconditions
pertaining to a production or to the total number of productions.
As mentioned earlier, another way to visually specify production preconditions is possible. The resulting equivalent alternative scheme is shown in Figure 2.
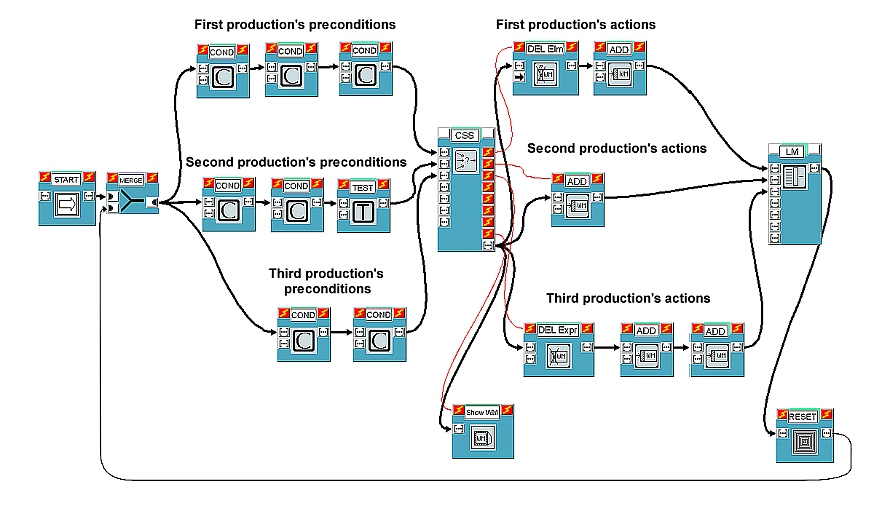
In this case, CS blocks are no longer used, since list L is analyzed and
modified little by little by condition and test blocks themselves. In a
certain sense, we may say that what was previously done by CC blocks is now
accomplished in a distributed manner. Practically, as soon as a condition or
test block does not match working memory, it gives a list with the
ok field set to zero out. On the other hand, every condition or
test block simply emits the list it receives as input (as it is) if the
corresponding ok field is null. In this manner, CSS receives the
same lists as in the previous scheme as inputs and system behavior is
identical (although a RESET block reinitializing some elements of L is now
necessary between the LM's output and the MERGE block's input). While in this
case common conditions have to be repeated, it is probably simpler to
identify and possibly add or delete conditions pertaining to a particular
production.
As regards building blocks, two cases can be distinguished: 1) the programmer already disposes of the blocks to be used for program construction (provided by someone else); 2) the programmer has to build the particular application's blocks.
The first may be the case when the program is part of a well defined and possibly wide context, for which particular conditions and actions --collected into a library-- have been foreseen. Otherwise when, for teaching purposes, the beginner is required to build productions by using pre-prepared conditions and actions (like for a puzzle). In those cases, blocks can reflect conditions or actions they represent through their titles or icons, properly set up.
The second case --which is the most generic-- implies an active but all in
all limited programmer intervention for block creation. The simplest way to
achieve this purpose is to specify, in the standard block, the default value
for the condition or action input. Such an operation can be accomplished in a
very simple manner, by opening the block's information window and typing the
desired value into the provided input field. Moreover, it is also possible to
build new blocks, starting from the standard ones, by using the library
creation program which is part of the VIPERS project. In this case too,
however, the programmer's task is very simple: it is enough to type the
desired condition or action instead of the one present in the variable
assignment at the first line of the Tcl script characterizing the block
(such a line is of the type: "set CONDITION ..." or
"set ELEMENT ..."). In this way, the block's title and/or icon
can be set up according to what it is intended to mean.
List L contains both past and present information and may be viewed as in-motion knowledge. Working memory and the list of the activated exemplars could have been represented by global static data in an ad-hoc system. However, we preferred to use an existing general purpose visual language as an implementation base. This was due to two main reasons. First, we desired to explore the potential of the data-flow paradigm in simulating symbolic computing system behavior. Secondly, we wanted to build our system in a quick and easy manner, by exploiting VIPERS ready-made features. Moreover, it is to be noted that through a system of such a type production-rule-based programs can be easily integrated within more general data-flow applications. For example, block Show WM in Figures 1 and 2, which is activated at the end of the computation, could be replaced with a block extracting some results from working memory. These results could then become inputs for other program subgraphs (not based on the production-rule paradigm).
The various links connecting blocks represent the visual program's data flow but also exert a computational control (control flow) over the production program being simulated. Thus, the inferential engine is implemented in a distributed manner by the different block functionalities.
Had we used a pure data-flow visual language instead of VIPERS, activation signals could not have been exploited by block CSS to activate the proper action sequence. However, we could also have used another type of CSS block, in which each output signal is replaced with a boolean output port. In this case, each action block would receive and emit a boolean value as well, which would be utilized to decide whether the corresponding action is to be executed or not (in a similar way to precondition analysis in the scheme shown in Figure 2). Only that CSS port relative to the chosen sequence would be set to true and system behavior, apart from a slight slowing down in execution, would not change.
Referring to the first method described for building productions, we can
formalize the functions represented by the various types of blocks as
follows:
| (a) | START: -> Linit |
| (f) | CSS: LNEW-1 X LNEW-2
X ... X LNEW-np -> L' |
| (g) | DEL Elmi,j:
Li,j-1 X n -> Li,j |
| (h) | DEL Expri,j:
Li,j-1 X pattern
-> Li,j |
| (i) | ADDi,j: Li,j-1
X pattern -> Li,j |
| (j) | LM: L1 |
L2 | ... |
Lnp -> Lprev |
Function (a) relates to block START. It has no arguments and as a result yields the initial data list, containing the working memory initial state.
Function (b) relates to block MERGE. It has the initial data list as an argument (if execution has just started) or the list emitted by block LM and as a result yields the argument list.
Function (c) relates to condition blocks C. It has no arguments and as a result yields the particular condition pattern represented by the block.
Function (d) relates to test blocks T and has no arguments. As a result, it yields the particular test pattern represented by the block.
Function (e) relates to condition collector blocks CC (index i
refers to the i-th production rule). It has as arguments the data list L and
the set of condition and test patterns relative to the production. As a
result, it yields a new list LNEW-i, where elements
ok, ENVs, TAGs, n_cond
and n_test have been modified according to the analysis carried
out (see Section 4.1).
Function (f) relates to the Conflict Set Solver
block CSS. It has the various LNEW lists emitted by
CC blocks as arguments and as a result yields a list L', already described in
Section 4.1 (np is the total number of productions).
Function (g) relates to action blocks DEL Elm (indexes i
and j refer to the j-th action of the i-th production). As
arguments it has list Li,j-1 emitted by the
previous action (or by block CSS if j = 1) and an integer number n
indicating that the working memory's element which matches the n-th
precondition of the production (according to the bond environment created)
is to be deleted. As a result it yields a new list Li,j,
whose WM component will lack the element removed.
Function (h) relates to action blocks DEL Expr (indexes i and j refer to the j-th action of the i-th production). As arguments it has the list Li,j-1 emitted by the previous action (or by block CSS if j = 1) and a pattern. The working memory's element matching this pattern will be deleted, according to the bond environment created. As a result it yields a new list Li,j, whose WM component will lack the element removed.
Function (i) relates to action blocks ADD (indexes i and j refer to
the j-th action of the i-th production). As arguments it has the list
Li,j-1 emitted by the previous action (or by block
CSS if j = 1) and a pattern. Variables of this pattern which have been
bounded during preconditions analysis will be substituted by the
corresponding constant values. As a result it yields a new list Li,j,
whose WM component will also hold the new element added.
Function (j) relates to the Lists Merge block LM.
As an argument it has the L list emitted by the last action of the activated
production and yields this list as a result (np is the total
number of productions).
Referring to the second described method for building productions, we may
formalize the functions represented by blocks COND and TEST as follows:
| (k) | CONDi,j:
Li,j-1 -> Li,j |
| (l) | TESTi,j:
Li,j-1 -> Li,j |
Functions (k) and (l) relates to condition and test blocks COND and TEST (indexes i and j refer to the j-th condition or test pattern of the i-th production). As an argument they have list Li,j-1 emitted by the previous condition or test block (or by block MERGE if j = 1) and yield as a result a new list Li,j, in which elements ok, ENVs, TAGs, n_cond and n_test have been modified according to the analysis carried out by the block (see Section 4.2).
Three simple examples will be now presented, to illustrate how the described visual system can be used to compose productions in real situations. In the examples, titles of condition and action blocks have been set to the conditions or actions they stand for, to allow an unskilled beginner programmer to easily compose the productions in a puzzle-like fashion (which proves to be especially useful at the very beginning of the learning stage).
The solution to the problem requires the three rules shown in Figure 3, based on the lex strategy (expr is the Tcl command for executing arithmetic calculations).
| START | CALCULATE | END |
|---|---|---|
power ?x ?y
|
power ?x ?y
|
power ?x ?y
|
The corresponding visual representation of these rules, complying with the first scheme discussed, is shown in Figure 4.
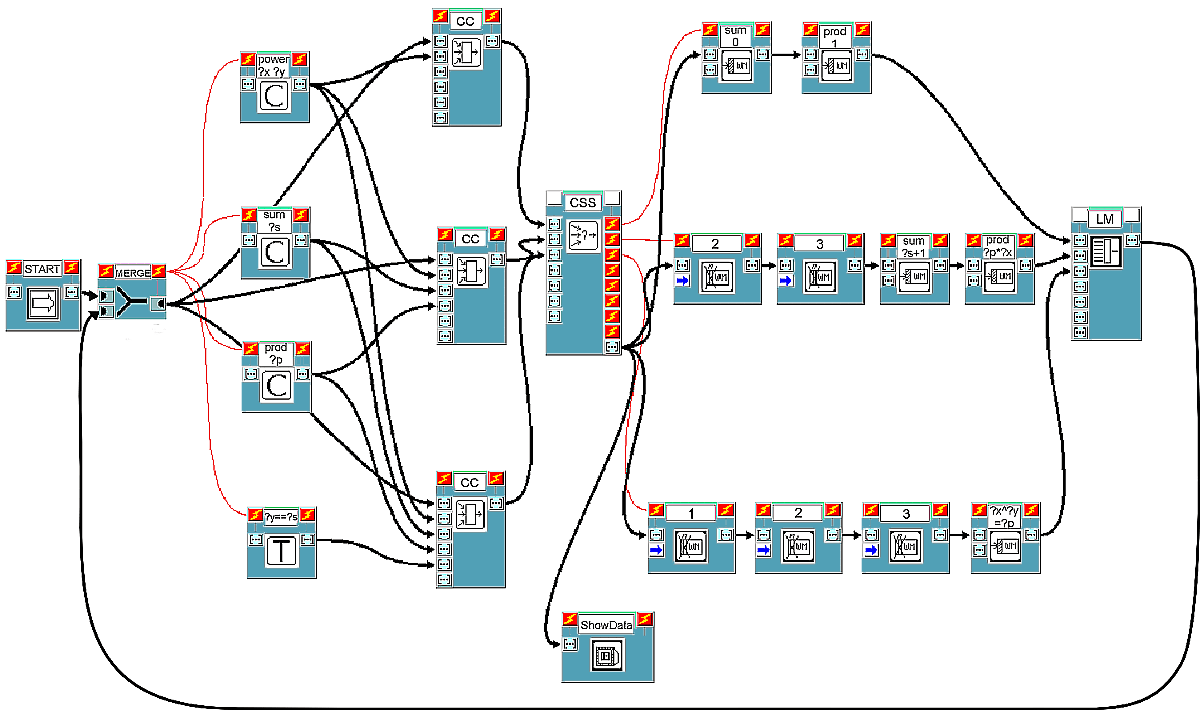
Block START settles the initial content of working memory (which can be set by opening the block's information window and which will be of the type: "power 3 4").
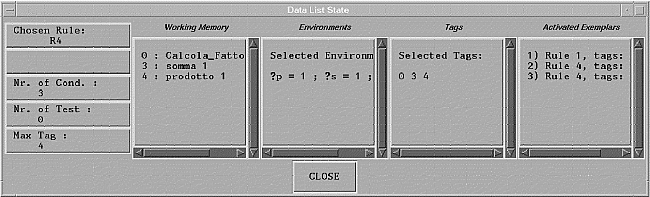
At every computational cycle, monitor block Show-Data displays the current contents of working memory and other information contained in the data list (see Figure 7). Blocks of this type can be inserted everywhere in the visual program, allowing system evolution to be properly understood. This feature too is particularly useful for the beginner. In fact, by deciding which parts of the visual program to debug, he or she can have a better control over the system which is being built.
Including also the case in which the number whose factorial is to be calculated is negative or equal to zero, and assuming that the lex strategy will still be used, the problem will be solved by the five productions shown in Figure 5.
| START | ZERO | END |
|---|---|---|
CF ?n
|
CF ?n
|
CF ?n
|
| CALCULATE | NEGATIVE |
|---|---|
CF ?n
|
CF ?n
|
The corresponding visual program, which complies with the second scheme described, is shown in Figure 6.
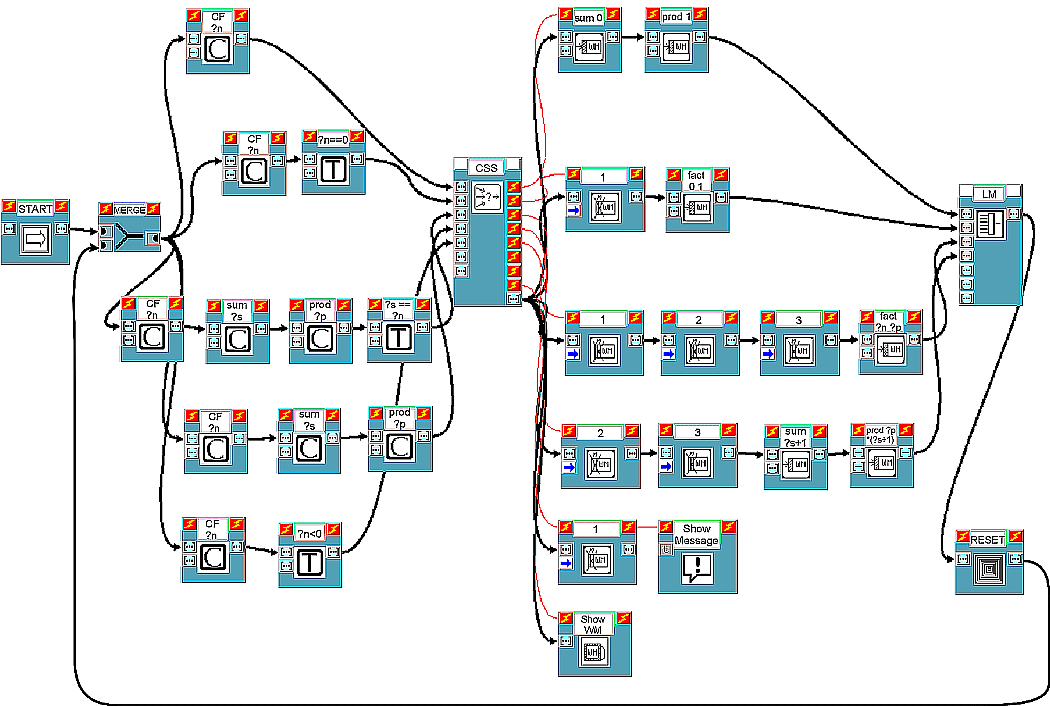
Initially, the content of the working memory, set by block START, will be of the type: 'CF 3', which indicates that the factorial of 3 must be calculated. Figure 7 shows an example of pieces of information which can be displayed by a monitor block during computation.
Suppose to have a simple database containing tuples of the type:
P <id> <price>
indicating that the price of a certain product identified by a code <id> is <price>. Suppose that the database, which makes up the working memory's contents, is to be analyzed to:
Figure 8 shows the three rules necessary to solve the problem.
| DELETE DUPLICATES | VERIFY INCONSISTENCIES | FIND MAXIMUM PRICE |
|---|---|---|
?t1 {P ?i ?p}
|
P ?i ?p1
|
Pmax ?i1 ?pm
|
The corresponding visual program, complying with the second scheme described, is shown in Figure 9.
In a conventional associative system for symbolic computing, the programmer has to textually build (write) productions, by using a more or less sophisticated editor. If program behavior is not what was expected, it becomes necessary to add, delete or modify productions. Changes, in turn, may imply additions, eliminations or transfers of conditions and/or actions from one production to the other. Thanks to the visual organization that the program acquires once it has been built using the described system, all these operations are considerably sped up. The programmer can easily delete or transfer condition, test and action blocks, by a few clicks of the mouse.
However, it is important to emphasize that the described system should not be thought of as something to be utilized by a skilled programmer (also because of the inefficiency that use of a list data structure would imply in case of complex programs): of course, an ad-hoc visual environment would be much more effective. Instead, besides being the occasion for a theoretical investigation, it aims at being a mechanism which allows the unskilled beginner to easily try out principles and features of production-rule-based programming.
[1] Larkin, J. H., Simon, H. A., "Why a Diagram is (Sometimes) Worth Ten Thousand Words". Cognitive Science, 1987, pp. 65-99.
[2] Hirakawa, M., Ichikawa, T., "Visual Language Studies - A Perspective", Software - Concepts and Tools, 1994, pp. 61-67.
[3] Koedinger, K.R, "Emergent Properties and Structural Constraints: Advantages of Diagrammatic Representations for Reasoning and Learning", in Proceedings of the AAAI Symposium on Diagrammatic Reasoning, Stanford University, 1992, March 25-27, pp. 154-159.
[4] Menzies, T., "Frameworks for Accessing Visual Languages", Technical Report TR95-35, 1996, Dept. of Software Development, Monash University, Melbourne, Australia.
[5] Reiss, S.P., "Working in the Garden Environment for Conceptual Programming", IEEE Software, November 1987, pp. 16-27.
[6] Ladret, D., Rueher, M., "VLP: a Visual Logic Programming Language", Journal of Visual Languages and Computing, 2, 1991, pp. 163-188.
[7] Pau, L, Olason, H., "Visual Logic Programming", Journal of Visual Languages and Computing, 2, 1991, pp. 3-15.
[8] Vose, G.M., "LabView: Laboratory Virtual Instrument Engineering Workbench", BYTE, vol. 11, n. 9, 1986, pp. 82-84.
[9] Gaines, B.R. (Fayyad, U.M.; Piatetsky-Shapiro, G.; Smyth, P.; and Uthurusamy, R. eds.), Transforming Rules and Trees into Comprehensible Knowledge Structures. Advances in Knowledge Discovery and Data Mining, 1996, pp. 205-226, Cambridge, Massachussets: MIT Press.
[10] Hübscher, R., "Composing Complex Behavior from Simple Visual Descriptions", in Proceedings of the 12th IEEE Symposium on Visual Languages, September 1996, Boulder, CO, USA, pp. 88-94.
[11] Bernini, M, Mosconi, M., "VIPERS: a Data-Flow Visual Programming Environment Based on the Tcl Language", in Proceedings of the 1994 AVI Conference, ACM Press.
[12] Ousterhout, J., Tcl and the Tk Toolkit. Addison Wesley, 1994.
[13] Erwig, M., Meyer, B., "Heterogeneus Visual Languages -Integrating Visual and Textual Programming-", in Proceedings of the 1995 IEEE Symposium on Visual Languages, pp. 318-325.
[14] Brownston, L., Farrel, F., Kant, E., Martin, N., Programming expert systems in OPS5: An introduction to rule-based programming. Addison Wesley, 1985, Reading, Massachussets.
This paper is also available in PostScript and PDF formats:
| zipped postscript (size 804 Kb) | PDF (size 488 Kb) |